Introduction

Casting is a manufacturing process in which liquid material is poured into a mold to solidify. Many types of defects or unwanted irregularities can occur during this process. The industry has its quality inspection department to remove defective products from the production line, but this is very time consuming since it is carried out manually. Furthermore, there is a chance of misclassifying due to human error, causing rejection of the whole product order.

In this post, let us build a model by training top-view images of a casted submersible pump impeller using a Convolutional Neural Network (CNN) so that it can distinguish accurately between defect from the ok one.

We will break down into several steps:

  1. Load the images and apply the data augmentation technique

  2. Visualize the images

  3. Training with validation: define the architecture, compile the model, model fitting and evaluation

  4. Testing on unseen images

  5. Make a conclusion

Note: This post is extracted from Kaggle Notebook: Casting Inspection with Data Augmentation (CNN)

Import Libraries

As usual, before we begin any analysis and modeling, let's import several necessary libraries to work with the data.

import pandas as pd
import numpy as np

# visualization
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# neural network model
from keras.callbacks import ModelCheckpoint
from keras.layers import *
from keras.models import Sequential, load_model
from keras.preprocessing.image import ImageDataGenerator

# evaluation
from sklearn.metrics import confusion_matrix, classification_report

Using TensorFlow backend.

Load the Images

Here is the structure of our folder containing image data:

casting_data
├───test
│   ├───def_front
│   └───ok_front
└───train
    ├───def_front
    └───ok_front

The folder casting_data consists of two subfolders test and train in which each of them has another subfolder: def_front and ok_front denoting the class of our target variable. The images inside train will be used for model fitting and validation, while test will be used purely for testing the model performance on unseen images.

Data Augmentation

We apply on-the-fly data augmentation, a technique to expand the training dataset size by creating a modified version of the original image which can improve model performance and the ability to generalize. This can be achieved by using ImageDataGenerator provided by keras with the following parameters:

  • rotation_range: Degree range for random rotations. We choose 360 degrees since the product is a round object.
  • width_shift_range: Fraction range of the total width to be shifted.
  • height_shift_range: Fraction range of the total height to be shifted.
  • shear_range: Degree range for random shear in a counter-clockwise direction.
  • zoom_range: Fraction range for random zoom.
  • horizontal_flip and vertical_flip are set to True for randomly flip image horizontally and vertically.
  • brightness_range: Fraction range for picking a brightness shift value.

Other parameters:

  • rescale: Rescale the pixel values to be in range 0 and 1.
  • validation_split: Reserve 20% of the training data for validation, and the rest 80% for model fitting.
train_generator = ImageDataGenerator(rotation_range=360,
                                     width_shift_range=0.05,
                                     height_shift_range=0.05,
                                     shear_range=0.05,
                                     zoom_range=0.05,
                                     horizontal_flip=True,
                                     vertical_flip=True,
                                     brightness_range=[0.75, 1.25],
                                     rescale=1./255,
                                     validation_split=0.2)

We define another set of value for the flow_from_directory parameters:

  • IMAGE_DIR: The directory where the image data is stored.
  • IMAGE_SIZE: The dimension of the image (300 px by 300 px).
  • BATCH_SIZE: Number of images that will be loaded and trained at one time.

  • SEED_NUMBER: Ensure reproducibility.

  • color_mode="grayscale": Treat our image with only one channel color.

  • class_mode and classes define the target class of our problem. In this case, we denote the defect class as positive (1), and ok as a negative class.
  • shuffle=True to make sure the model learns the defect and ok images alternately.
IMAGE_DIR = "/kaggle/input/real-life-industrial-dataset-of-casting-product/casting_data/"
IMAGE_SIZE = (300, 300)
BATCH_SIZE = 64
SEED_NUMBER = 123

gen_args = dict(target_size=IMAGE_SIZE,
                color_mode="grayscale",
                batch_size=BATCH_SIZE,
                class_mode="binary",
                classes={"ok_front": 0, "def_front": 1},
                shuffle=True,
                seed=SEED_NUMBER)

train_dataset = train_generator.flow_from_directory(directory=IMAGE_DIR + "train",
                                                    subset="training", **gen_args)
validation_dataset = train_generator.flow_from_directory(directory=IMAGE_DIR + "train",
                                                         subset="validation", **gen_args)

Found 5307 images belonging to 2 classes.
Found 1326 images belonging to 2 classes.

Important: We must not perform any data augmentation on the test data, since we want to test our model performance when applied on the real scenario. The rescaling is done to ensure mathematical stability when training the model. 
test_generator = ImageDataGenerator(rescale=1./255)
test_dataset = test_generator.flow_from_directory(directory=IMAGE_DIR + "test",
                                                  **gen_args)

Found 715 images belonging to 2 classes.

Image Data Proportion

We successfully load and apply on-the-fly data augmentation according to the specified parameters. Now, let's take a look on how is the proportion of the train, validation, and test image for each class.

image_data = [{"data": typ,
               "class": name.split('/')[0],
               "filename": name.split('/')[1]}
              for dataset, typ in zip([train_dataset, validation_dataset, test_dataset], ["train", "validation", "test"])
              for name in dataset.filenames]
image_df = pd.DataFrame(image_data)
data_crosstab = pd.crosstab(index=image_df["data"],
                            columns=image_df["class"],
                            margins=True,
                            margins_name="Total")
data_crosstab
class def_front ok_front Total
data
test 453 262 715
train 3007 2300 5307
validation 751 575 1326
Total 4211 3137 7348 

total_image = data_crosstab.iloc[-1, -1]
ax = data_crosstab.iloc[:-1, :-1].T.plot(kind="bar", stacked=True, rot=0)

percent_val = []

for rect in ax.patches:
    height = rect.get_height()
    width = rect.get_width()
    percent = 100*height/total_image

    ax.text(rect.get_x() + width - 0.25,
            rect.get_y() + height/2,
            int(height),
            ha='center',
            va='center',
            color="white",
            fontsize=10)

    ax.text(rect.get_x() + width + 0.01,
            rect.get_y() + height/2,
            "{:.2f}%".format(percent),
            ha='left',
            va='center',
            color="black",
            fontsize=10)

    percent_val.append(percent)

handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=labels)

percent_def = sum(percent_val[::2])
ax.set_xticklabels(["def_front\n({:.2f} %)".format(
    percent_def), "ok_front\n({:.2f} %)".format(100-percent_def)])
plt.title("IMAGE DATA PROPORTION", fontsize=15, fontweight="bold")
plt.show()

We will proceed to the next step, since the proportion of data can be considered as balanced.

Visualize the Image

In this section, we visualize the image to make sure that it is loaded correctly.

Visualize Image in Batch

Visualize the first batch (BATCH_SIZE = 64) of the training dataset (images with data augmentation) and also the test dataset (images without data augmentation).

mapping_class = {0: "ok", 1: "defect"}

def visualizeImageBatch(dataset, title):
    images, labels = next(iter(dataset))
    images = images.reshape(BATCH_SIZE, *IMAGE_SIZE)
    fig, axes = plt.subplots(8, 8, figsize=(16, 16))

    for ax, img, label in zip(axes.flat, images, labels):
        ax.imshow(img, cmap="gray")
        ax.axis("off")
        ax.set_title(mapping_class[label], size=20)

    plt.tight_layout()
    fig.suptitle(title, size=30, y=1.05, fontweight="bold")
    plt.show()

    return images


train_images = visualizeImageBatch(
    train_dataset,
    "FIRST BATCH OF THE TRAINING IMAGES\n(WITH DATA AUGMENTATION)")


test_images = visualizeImageBatch(
    test_dataset,
    "FIRST BATCH OF THE TEST IMAGES\n(WITHOUT DATA AUGMENTATION)")

Visualize Detailed Image

Let's also take a look on the detailed image by each pixel. Instead of plotting 300 pixels by 300 pixels (which computationally expensive), we take a small part of 25 pixels by 25 pixels only.

img = np.squeeze(train_images[4])[75:100, 75:100]

fig = plt.figure(figsize=(15, 15))
ax = fig.add_subplot(111)
ax.imshow(img, cmap="gray")
ax.axis("off")

w, h = img.shape
for x in range(w):
    for y in range(h):
        value = img[x][y]
        ax.annotate("{:.2f}".format(value), xy=(y, x),
                    horizontalalignment="center",
                    verticalalignment="center",
                    color="white" if value < 0.4 else "black")

These are the example of values that we are going to feed into our CNN architecture.

Training the Network

As mentioned earlier, we are going to train a CNN model to classify the casting product image. CNN is used as an automatic feature extractor from the images so that it can learn how to distinguish between defect and ok casted products. It effectively uses the adjacent pixel to downsample the image and then use a prediction (fully-connected) layer to solve the classification problem. This is a simple illustration by Udacity on how the layers are arranged sequentially:

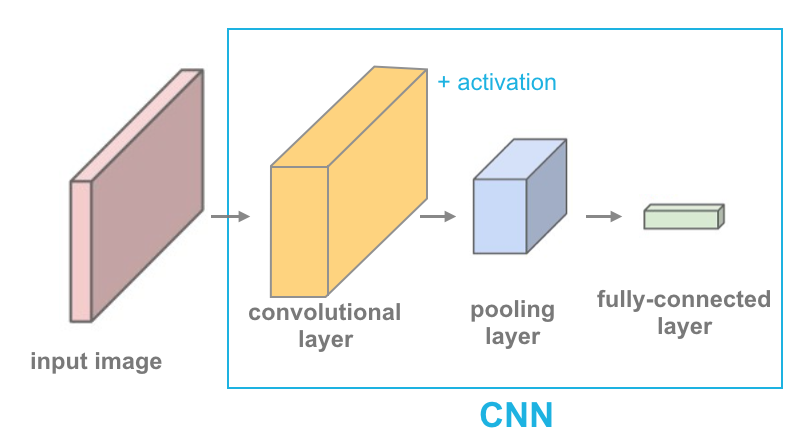
Define Architecture

Here is the detailed architecture that we are going to use:

  1. First convolutional layer: consists of 32 filters with kernel_size matrix 3 by 3. Using 2-pixel strides at a time, reduce the image size by half.
  2. First pooling layer: Using max-pooling matrix 2 by 2 (pool_size) and 2-pixel strides at a time further reduce the image size by half.
  3. Second convolutional layer: Just like the first convolutional layer but with 16 filters only.
  4. Second pooling layer: Same as the first pooling layer.
  5. Flattening: Convert two-dimensional pixel values into one dimension, so that it is ready to be fed into the fully-connected layer.
  6. First dense layer + Dropout: consists of 128 units and 1 bias unit. Dropout of rate 20% is used to prevent overfitting.
  7. Second dense layer + Dropout: consists of 64 units and 1 bias unit. Dropout of rate 20% is also used to prevent overfitting.
  8. Output layer: consists of only one unit and activation is a sigmoid function to convert the scores into a probability of an image being defect.

For every layer except output layer, we use Rectified Linear Unit (ReLU) activation function as follow:

Note: ReLU is commonly used as an activation function for image classification. The purpose is to introduce non-linearity to our model so that it can capture non-linear features of an image (example: pixel transition, image borders, colors, etc). 
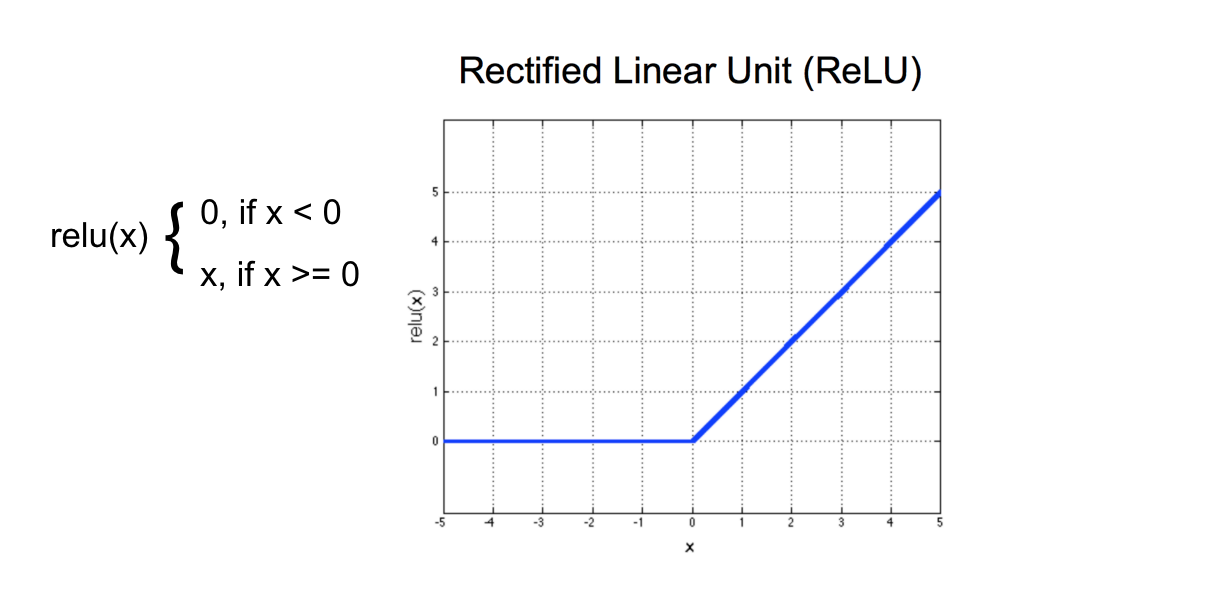
model = Sequential(
    [
        # First convolutional layer
        Conv2D(filters=32,
               kernel_size=3,
               strides=2,
               activation="relu",
               input_shape=IMAGE_SIZE + (1, )),

        # First pooling layer
        MaxPooling2D(pool_size=2,
                     strides=2),

        # Second convolutional layer
        Conv2D(filters=16,
               kernel_size=3,
               strides=2,
               activation="relu"),

        # Second pooling layer
        MaxPooling2D(pool_size=2,
                     strides=2),

        # Flattening
        Flatten(),

        # Fully-connected layer
        Dense(128, activation="relu"),
        Dropout(rate=0.2),

        Dense(64, activation="relu"),
        Dropout(rate=0.2),

        Dense(1, activation="sigmoid")
    ]
)

model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 149, 149, 32)      320       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 36, 36, 16)        4624      
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 18, 18, 16)        0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 5184)              0         
_________________________________________________________________
dense_1 (Dense)              (None, 128)               663680    
_________________________________________________________________
dropout_1 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 64)                8256      
_________________________________________________________________
dropout_2 (Dropout)          (None, 64)                0         
_________________________________________________________________
dense_3 (Dense)              (None, 1)                 65        
=================================================================
Total params: 676,945
Trainable params: 676,945
Non-trainable params: 0
_________________________________________________________________

Compile the Model

Next, we specify how the model backpropagates or update the weights after each batch feed-forward. We use Adam optimizer and a loss function binary cross-entropy since we are dealing with binary classification problem. The metrics used to monitor the training progress is accuracy.

model.compile(optimizer="adam",
              loss="binary_crossentropy",
              metrics=["accuracy"])

Model Fitting

For each epoch, batch_size $\times$ steps_per_epoch images will be fed into our CNN architecture. In this case, we specify the steps_per_epoch to be 150 so for each epoch 64 * 150 = 9600 augmented images from the training dataset will be fed. We let the model train for 25 epochs.

By using ModelCheckpoint, the best model will be automatically saved if the current val_loss is lower than the previous one.

STEPS = 150

checkpoint = ModelCheckpoint("cnn_casting_inspection_model.hdf5",
                             verbose=1,
                             save_best_only=True,
                             monitor="val_loss")

model.fit_generator(generator=train_dataset,
                    validation_data=validation_dataset,
                    steps_per_epoch=STEPS,
                    epochs=25,
                    validation_steps=STEPS,
                    callbacks=[checkpoint],
                    verbose=1)

Epoch 1/25
150/150 [==============================] - 166s 1s/step - loss: 0.6243 - accuracy: 0.6327 - val_loss: 0.5896 - val_accuracy: 0.7033

Epoch 00001: val_loss improved from inf to 0.58961, saving model to cnn_casting_inspection_model.hdf5
Epoch 2/25
150/150 [==============================] - 150s 1000ms/step - loss: 0.5075 - accuracy: 0.7515 - val_loss: 0.4829 - val_accuracy: 0.8062

Epoch 00002: val_loss improved from 0.58961 to 0.48288, saving model to cnn_casting_inspection_model.hdf5
Epoch 3/25
150/150 [==============================] - 151s 1s/step - loss: 0.3580 - accuracy: 0.8378 - val_loss: 0.3844 - val_accuracy: 0.8882

Epoch 00003: val_loss improved from 0.48288 to 0.38443, saving model to cnn_casting_inspection_model.hdf5
Epoch 4/25
150/150 [==============================] - 151s 1s/step - loss: 0.2687 - accuracy: 0.8818 - val_loss: 0.2590 - val_accuracy: 0.9073

Epoch 00004: val_loss improved from 0.38443 to 0.25899, saving model to cnn_casting_inspection_model.hdf5
Epoch 5/25
150/150 [==============================] - 149s 991ms/step - loss: 0.1998 - accuracy: 0.9177 - val_loss: 0.1309 - val_accuracy: 0.9443

Epoch 00005: val_loss improved from 0.25899 to 0.13093, saving model to cnn_casting_inspection_model.hdf5
Epoch 6/25
150/150 [==============================] - 148s 988ms/step - loss: 0.1671 - accuracy: 0.9350 - val_loss: 0.1323 - val_accuracy: 0.9442

Epoch 00006: val_loss did not improve from 0.13093
Epoch 7/25
150/150 [==============================] - 149s 995ms/step - loss: 0.1447 - accuracy: 0.9443 - val_loss: 0.0580 - val_accuracy: 0.9619

Epoch 00007: val_loss improved from 0.13093 to 0.05799, saving model to cnn_casting_inspection_model.hdf5
Epoch 8/25
150/150 [==============================] - 148s 988ms/step - loss: 0.1187 - accuracy: 0.9529 - val_loss: 0.0362 - val_accuracy: 0.9657

Epoch 00008: val_loss improved from 0.05799 to 0.03623, saving model to cnn_casting_inspection_model.hdf5
Epoch 9/25
150/150 [==============================] - 149s 991ms/step - loss: 0.1728 - accuracy: 0.9289 - val_loss: 0.0996 - val_accuracy: 0.9357

Epoch 00009: val_loss did not improve from 0.03623
Epoch 10/25
150/150 [==============================] - 148s 990ms/step - loss: 0.1121 - accuracy: 0.9578 - val_loss: 0.0628 - val_accuracy: 0.9673

Epoch 00010: val_loss did not improve from 0.03623
Epoch 11/25
150/150 [==============================] - 149s 995ms/step - loss: 0.0880 - accuracy: 0.9688 - val_loss: 0.0164 - val_accuracy: 0.9757

Epoch 00011: val_loss improved from 0.03623 to 0.01642, saving model to cnn_casting_inspection_model.hdf5
Epoch 12/25
150/150 [==============================] - 149s 991ms/step - loss: 0.0902 - accuracy: 0.9667 - val_loss: 0.1463 - val_accuracy: 0.9571

Epoch 00012: val_loss did not improve from 0.01642
Epoch 13/25
150/150 [==============================] - 150s 997ms/step - loss: 0.0884 - accuracy: 0.9678 - val_loss: 0.1241 - val_accuracy: 0.9726

Epoch 00013: val_loss did not improve from 0.01642
Epoch 14/25
150/150 [==============================] - 148s 986ms/step - loss: 0.0834 - accuracy: 0.9703 - val_loss: 0.1530 - val_accuracy: 0.9615

Epoch 00014: val_loss did not improve from 0.01642
Epoch 15/25
150/150 [==============================] - 149s 994ms/step - loss: 0.0906 - accuracy: 0.9661 - val_loss: 0.0405 - val_accuracy: 0.9747

Epoch 00015: val_loss did not improve from 0.01642
Epoch 16/25
150/150 [==============================] - 146s 973ms/step - loss: 0.0789 - accuracy: 0.9716 - val_loss: 0.0140 - val_accuracy: 0.9809

Epoch 00016: val_loss improved from 0.01642 to 0.01395, saving model to cnn_casting_inspection_model.hdf5
Epoch 17/25
150/150 [==============================] - 152s 1s/step - loss: 0.0623 - accuracy: 0.9795 - val_loss: 0.1122 - val_accuracy: 0.9791

Epoch 00017: val_loss did not improve from 0.01395
Epoch 18/25
150/150 [==============================] - 148s 984ms/step - loss: 0.0545 - accuracy: 0.9813 - val_loss: 0.1440 - val_accuracy: 0.9848

Epoch 00018: val_loss did not improve from 0.01395
Epoch 19/25
150/150 [==============================] - 150s 999ms/step - loss: 0.0562 - accuracy: 0.9801 - val_loss: 0.0300 - val_accuracy: 0.9849

Epoch 00019: val_loss did not improve from 0.01395
Epoch 20/25
150/150 [==============================] - 149s 994ms/step - loss: 0.0670 - accuracy: 0.9766 - val_loss: 0.0938 - val_accuracy: 0.9814

Epoch 00020: val_loss did not improve from 0.01395
Epoch 21/25
150/150 [==============================] - 148s 984ms/step - loss: 0.0536 - accuracy: 0.9819 - val_loss: 0.0242 - val_accuracy: 0.9854

Epoch 00021: val_loss did not improve from 0.01395
Epoch 22/25
150/150 [==============================] - 152s 1s/step - loss: 0.0507 - accuracy: 0.9843 - val_loss: 0.0155 - val_accuracy: 0.9794

Epoch 00022: val_loss did not improve from 0.01395
Epoch 23/25
150/150 [==============================] - 150s 997ms/step - loss: 0.0574 - accuracy: 0.9823 - val_loss: 0.0657 - val_accuracy: 0.9807

Epoch 00023: val_loss did not improve from 0.01395
Epoch 24/25
150/150 [==============================] - 148s 987ms/step - loss: 0.0535 - accuracy: 0.9826 - val_loss: 0.0534 - val_accuracy: 0.9861

Epoch 00024: val_loss did not improve from 0.01395
Epoch 25/25
150/150 [==============================] - 149s 994ms/step - loss: 0.0545 - accuracy: 0.9821 - val_loss: 0.0111 - val_accuracy: 0.9842

Epoch 00025: val_loss improved from 0.01395 to 0.01115, saving model to cnn_casting_inspection_model.hdf5

<keras.callbacks.callbacks.History at 0x7f55c3542160>

Note: The model achieves 98.21% accuracy on training dataset and 98.42% on validation dataset.

Training Evaluation

Let's plot both loss and accuracy metrics for train and validation data based on each epoch.

plt.subplots(figsize=(8, 6))
sns.lineplot(data=pd.DataFrame(
    model.history.history,
    index=range(1, 1+len(model.history.epoch))))
plt.title("TRAINING EVALUATION", fontweight="bold", fontsize=20)
plt.xlabel("Epochs")
plt.ylabel("Metrics")

plt.legend(labels=['val loss', 'val accuracy', 'train loss', 'train accuracy'])
plt.show()

Note: We can conclude that the model is not overfitting the data since both train loss and val loss simultaneously dropped towards zero. Also, both train accuracy and val accuracy increases towards 100%.

Testing on Unseen Images

Our model performs very well on the training and validation dataset which uses augmented images. Now, we test our model performance with unseen and unaugmented images.

best_model = load_model("/kaggle/working/cnn_casting_inspection_model.hdf5")
y_pred_prob = best_model.predict_generator(generator=test_dataset, verbose=1)

12/12 [==============================] - 2s 143ms/step

The output of the prediction is in the form of probability. We use THRESHOLD = 0.5 to separate the classes. If the probability is greater or equal to the THRESHOLD, then it will be classified as defect, otherwise ok.

THRESHOLD = 0.5
y_pred_class = (y_pred_prob >= THRESHOLD).reshape(-1,)
y_true_class = test_dataset.classes[test_dataset.index_array]

pd.DataFrame(
    confusion_matrix(y_true_class, y_pred_class),
    index=[["Actual", "Actual"], ["ok", "defect"]],
    columns=[["Predicted", "Predicted"], ["ok", "defect"]],
)
Predicted
ok defect
Actual ok 259 3
defect 1 452 

print(classification_report(y_true_class, y_pred_class, digits=4))

              precision    recall  f1-score   support

           0     0.9962    0.9885    0.9923       262
           1     0.9934    0.9978    0.9956       453

    accuracy                         0.9944       715
   macro avg     0.9948    0.9932    0.9940       715
weighted avg     0.9944    0.9944    0.9944       715

On test dataset, the model achieves a very good result as follow:

  • Accuracy: 99.44%
  • Recall: 99.78%
  • Precision: 99.34%
  • F1 score: 99.56%

Important: According to the problem statement, we want to minimize the case of False Negative, where the defect product is misclassified as ok. This can cause the whole order to be rejected and create a big loss for the company. Therefore, in this case, we prioritize Recall over Precision. But if we take into account the cost of re-casting a product, we have to minimize the case of False Positive also, where the ok product is misclassified as defect. Therefore we can prioritize the F1 score which combines both Recall and Precision.

Visualize the Results

Lastly, we visualize the results by comparing its true label with the predicted label and also provide the probability of each image being on the predicted class. A blue color on the text indicates that our model correctly classify the image, otherwise red color is used.

images, labels = next(iter(test_dataset))
images = images.reshape(BATCH_SIZE, *IMAGE_SIZE)
fig, axes = plt.subplots(4, 4, figsize=(16, 16))

for ax, img, label in zip(axes.flat, images, labels):
    ax.imshow(img, cmap="gray")
    true_label = mapping_class[label]

    [[pred_prob]] = best_model.predict(img.reshape(1, *IMAGE_SIZE, -1))
    pred_label = mapping_class[int(pred_prob >= THRESHOLD)]

    prob_class = 100*pred_prob if pred_label == "defect" else 100*(1-pred_prob)

    ax.set_title(f"TRUE LABEL: {true_label}", fontweight="bold", fontsize=18)
    ax.set_xlabel(f"PREDICTED LABEL: {pred_label}\nProb({pred_label}) = {(prob_class):.2f}%",
                  fontweight="bold", fontsize=15,
                  color="blue" if true_label == pred_label else "red")

    ax.set_xticks([])
    ax.set_yticks([])

plt.tight_layout()
fig.suptitle("TRUE VS PREDICTED LABEL FOR 16 RANDOM TEST IMAGES",
             size=30, y=1.03, fontweight="bold")
plt.show()

Since the proportion of correctly classified images is very large, let's also visualize the misclassified only.

misclassify_pred = np.nonzero(y_pred_class != y_true_class)[0]

fig, axes = plt.subplots(2, 2, figsize=(8, 8))

for ax, batch_num, image_num in zip(axes.flat, misclassify_pred // BATCH_SIZE, misclassify_pred % BATCH_SIZE):
    images, labels = test_dataset[batch_num]
    img = images[image_num]
    ax.imshow(img.reshape(*IMAGE_SIZE), cmap="gray")

    true_label = mapping_class[labels[image_num]]
    [[pred_prob]] = best_model.predict(img.reshape(1, *IMAGE_SIZE, -1))
    pred_label = mapping_class[int(pred_prob >= THRESHOLD)]

    prob_class = 100*pred_prob if pred_label == "defect" else 100*(1-pred_prob)

    ax.set_title(f"TRUE LABEL: {true_label}", fontweight="bold", fontsize=18)
    ax.set_xlabel(f"PREDICTED LABEL: {pred_label}\nProb({pred_label}) = {(prob_class):.2f}%",
                  fontweight="bold", fontsize=15,
                  color="blue" if true_label == pred_label else "red")

    ax.set_xticks([])
    ax.set_yticks([])

plt.tight_layout()
fig.suptitle(f"MISCLASSIFIED TEST IMAGES ({len(misclassify_pred)} out of {len(y_true_class)})",
             size=20, y=1.03, fontweight="bold")
plt.show()

Out of 715 test images, only 4 images are being misclassified.

Conclusion

By using CNN and on-the-fly data augmentation, the performance of our model in training, validation, and test images is almost perfect, reaching 98-99% accuracy and F1 score. We can utilize this model by embedding it into a surveillance camera where the system can automatically separate defective product from the production line. This method surely can reduce human error and human resources on manual inspection, but it still needs supervision from human since the model is not 100% correct at all times.